Short introduction to elliptic PDE

(if you don't need introduction go directly to this page…)

In this section, we discuss in more details numeric methods for solving elliptic PDE (for hyperbolic and parabolic problems the situation is quite similar – at least for our solver the computation schema is practically the same).

First of all, let’s note that any elliptic equation can be converted to its canonical form:

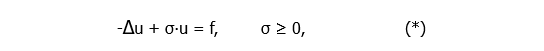
where ∆ is Laplace operator (for 2-dimension problem we have ∆ =).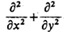

In case of σ = 0 and f = 0 we have a Laplace equation. If the right hand side of the equation f = f(x, y) is not zero, then it is called Poisson equation.

The typical problem, governed by Poisson equation, is the problem of calculating distribution of electrical field potential u = u(x, y) in the given region, with the given distribution of electric charges f = f(x, y).

The case σ = 0 corresponds to vacuum. For heterogeneous environment function σ = σ(x, y) define conduction of the field in the given region.

Functions f and σ are considered to be known, function u is unknown.

For numerical solving of elliptic equations, we apply discretization, based on finite differences method.
For simplicity we discuss only regular grid with equal step.

1. Discretization on a regular grid

   We begin with applying FDM approach to elliptic problems
   Read more…

2. Standard solvers

   Before discussing Marlin Solver let's look on standard approaches to solving elliptic equations.
   Read more…

PAY ATTENTION:

1. Marlin Solver approach

   In this section we discuss our way of solving PDE based on Marlin Solver.
   Read more…